Μην ακολουθείτε τις στατιστικές αναλύσεις στο ΤΖΟΚΕΡ καθώς η κληρωτίδα δεν έχει προτιμήσεις ούτε μνήμη (όλοι οι αριθμοί και οι συνδυασμοί αριθμών έχουν κάθε φορά την ίδια πιθανότητα κλήρωσης) και να θυμάστε οι παίκτες έχουν προτιμήσεις και μνήμη καθώς και ότι αντίπαλος δεν είναι η τύχη ούτε ο διοργανωτής, αλλά οι συμπαίκτες.
Παρακάτω θα αναλύσω τις πιθανότητες επιτυχίας του γνωστού παιχνιδιού ΤΖΟΚΕΡ του ΟΠΑΠ σύμφωνα με τον κλασικό ορισμό των πιθανοτήτων (κατά Laplace). Σύμφωνα με τον παραπάνω ορισμό κάνουμε την παραδοχή ότι όλες οι στήλες είναι ισοπίθανες και δεν υπάρχουν εξωγενείς παράγοντες που μπορούν να επηρεάσουν το αποτέλεσμα (π.χ. βάρος σφαιριδίων).
Μπορούμε να βρούμε τις πιθανότητες να πιάσουμε μόνο το 5άρι, χάνοντας το τζόκερ ως εξής: Οι πιθανότητες να πιάσουμε τον πρώτο αριθμό είναι 5 προς 45, δηλαδή 11%. Οι πιθανότητες να πιάσουμε τον δεύτερο αριθμό είναι 4 προς 44, δηλαδή 9% (βάζουμε 4 στον αριθμητή γιατί θεωρούμε πως πιάσαμε ήδη τον πρώτο αριθμό, οπότε έφυγε ο ένας αριθμός από τους πέντε που έχουμε ποντάρει. Επίσης, αφού στις κληρώσεις δεν γίνεται επανατοποθέτηση των σφαιρών στην κληρωτίδα, βάζουμε παρανομαστή 44 γιατί ήδη κληρώθηκε ένας αριθμός οπότε τώρα παίζουν 44 νούμερα). Οι πιθανότητες για τον τρίτο είναι 3 προς 43, δηλαδή 7%. Για τον τέταρτο 2 προς 42, δηλαδή 4,7% και για τον πέμπτο 1 προς 41, δηλαδή 2,4%. Για να βρούμε την πιθανότητα να πιάσουμε και τα πέντε νούμερα μαζί (δεσμευμένες πιθανότητες) πολλαπλασιάζουμε τις παραπάνω πιθανότητες και βγαίνει 0,000000818492, δηλαδή 0,000081% ή 0,81 πιθανότητες στο 1.000.000.
Κι αυτό χωρίς τον επιπλέον αριθμό τζόκερ. Αν θελήσουμε να συνυπολογίσουμε και το τζόκερ που είναι 1 προς 20 τότε οι πιθανότητες να πιάσει κανείς 5+1 παίζοντας ένα απλό δελτίο είναι 0,000004090755%, δηλαδή περίπου 4 πιθανότητες στα 100.000.000!
Πρέπει λοιπόν κανείς να παίξει 12.222 δελτία διαφορετικών συνδυασμών, για να έχει περίπου 1% πιθανότητα να κερδίσει απλό 5άρι. Αφού κάθε στήλη χωρίς σύστημα κοστίζει 50 λεπτά, συνεπώς πρέπει να δαπανήσει 6.111€. Αν ενδιαφέρεται κανείς να έχει περίπου 1% πιθανότητα να κερδίσει το 5+1, τότε πρέπει να παίξει 244.351 δελτία διαφορετικών συνδυασμών με κόστος 122.175,5€.
Επίσης, αν κάποιος θέλει να έχει 100% πιθανότητα να κερδίσει το 5άρι (χωρίς σύστημα πάντα) πρέπει να ξοδέψει 610.880€ σε 1.221.759 απλά δελτία διαφορετικών συνδυασμών και αν θέλει να έχει 100% πιθανότητα να κερδίσει το 5+1 πρέπει να ξοδέψει 12.217.590€ σε 24.435.180 διαφορετικά δελτία.
Τέλος, πρέπει να γνωρίζουμε πως κάποιος που παίζει συνεχώς τα ίδια νούμερα δεν έχει περισσότερες πιθανότητες να κερδίσει. Δεν υπάρχει κανένα απολύτως αβαντάζ αν παίζει τα ίδια νούμερα συνέχεια ή αν τα αλλάζει από κλήρωση σε κλήρωση. Δεν σημαίνει ότι επειδή δεν κληρώθηκε μέχρι τώρα ένας συγκεκριμένος συνδυασμός αριθμών, έχουν αυξηθεί οι πιθανότητες να πέσει κάποτε στο μέλλον. Κάθε κλήρωση είναι ανεξάρτητη από την προηγούμενη και οι αριθμοί της προηγούμενης κλήρωσης έχουν ακριβώς την ίδια πιθανότητα να ξανακληρωθούν.
Η πλάνη του τζογαδόρου (The Gambler’s fallacy) είναι η πεποίθηση ότι εάν υπάρχουν αποκλίσεις από την αναμενόμενη συμπεριφορά σε επανειλημμένες ανεξάρτητες δοκιμές κάποιας τυχαίας διαδικασίας, τότε οι αποκλίσεις αυτές είναι πιθανό να εξομαλυνθούν από αντίθετες αποκλίσεις στο μέλλον.
Για παράδειγμα αν ένα κέρμα ριχτεί επανειλημμένα και έρχεται «γράμματα» περισσότερες φορές από αυτές που αναμένονται, τότε ένας παίκτης μπορεί λανθασμένα να πιστέψει ότι σε μελλοντικές ρίψεις του νομίσματος το «κεφάλι» είναι πιο πιθανό να έρθει. Αυτή η προσδοκία είναι λανθασμένη για τον απλό λόγο ότι το σύμπαν δεν έχει μνήμη. Το αποτέλεσμα επαναλαμβανόμενων ρίψεων είναι στατιστικά ανεξάρτητο, δηλαδή η πιθανότητα να έρθει «κεφάλι» ή «γράμματα» είναι 50% σε κάθε ρίψη. Η πιθανότητα στην πρώτη ρίψη να έρθει «κεφάλι» είναι 1⁄2 και η πιθανότητα να έρθει πάλι «κεφάλι» στην δεύτερη ρίψη είναι 1⁄2×1⁄2 = 1⁄4, δηλαδή μία στις τέσσερις και η πιθανότητα να έρθει 3 φορές συνεχόμενα «κεφάλι» είναι 1⁄8 δηλαδή μία στις οχτώ = 0,5×0,5×0,5= 0,53 = 0.125 = 1⁄8 και για n ρίψεις η πιθανότητα να έρθει n φορές κεφάλι είναι 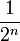 , όσοι και όλοι οι πιθανοί συνδυασμοί.
, όσοι και όλοι οι πιθανοί συνδυασμοί.
Ας υποθέσουμε ότι ρίξαμε «κεφάλι» 4 συνεχόμενες φορές και εάν ρίξουμε πάλι «κεφάλι» θα έχουμε 5 συνεχόμενες ρίψεις με αποτέλεσμα «κεφάλι». Η πιθανότητα όπως είδαμε να έρθει 5 φορές συνεχόμενες «κεφάλι» είναι 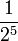 = 0,55 = 0.03125 = 1⁄32 = μια στις τριάντα δύο. Η πλάνη του τζογαδόρου είναι να πιστέψει ότι η πιθανότητα να έρθει «γράμματα» την πέμπτη φορά είναι μεγαλύτερη από το να έρθει «κεφάλι», προσδοκία εσφαλμένη καθώς η πιθανότητα για 5 φορές «κεφάλι» και η πιθανότητα για 4 φορές «κεφάλι» και μετά «γράμματα» είναι απόλυτα ίσες και είναι μια στις τριάντα δύο. Με 4 φορές «κεφάλι» η πιθανότητα να έρθει την πέμπτη φορά «γράμματα» είναι:
= 0,55 = 0.03125 = 1⁄32 = μια στις τριάντα δύο. Η πλάνη του τζογαδόρου είναι να πιστέψει ότι η πιθανότητα να έρθει «γράμματα» την πέμπτη φορά είναι μεγαλύτερη από το να έρθει «κεφάλι», προσδοκία εσφαλμένη καθώς η πιθανότητα για 5 φορές «κεφάλι» και η πιθανότητα για 4 φορές «κεφάλι» και μετά «γράμματα» είναι απόλυτα ίσες και είναι μια στις τριάντα δύο. Με 4 φορές «κεφάλι» η πιθανότητα να έρθει την πέμπτη φορά «γράμματα» είναι:  δηλαδή πάλι 50%.
δηλαδή πάλι 50%.
Από τα παραπάνω συμπεραίνουμε ότι εάν κάποιος ρίξει ένα νόμισμα για n=21 φορές, η πιθανότητα να έρθει 21 φορές «κεφάλι» είναι 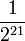 = 0,521 δηλαδή 1 στις 2.097.152 φορές, αλλά η πιθανότητα να έρθει «κεφάλι» την 21η φορά αφού έχει ήδη ρίξει 20 φορές «κεφάλι» είναι 1⁄2, δηλαδή όσες και να έρθει «γράμματα».
= 0,521 δηλαδή 1 στις 2.097.152 φορές, αλλά η πιθανότητα να έρθει «κεφάλι» την 21η φορά αφού έχει ήδη ρίξει 20 φορές «κεφάλι» είναι 1⁄2, δηλαδή όσες και να έρθει «γράμματα».
- πιθανότητα 20 φορές «κεφάλι» και μετά «γράμματα» = 0,520 × 0,5 = 0,521
- πιθανότητα 20 φορές «κεφάλι» και μετά πάλι «κεφάλι» = 0,520 × 0,5 = 0,521δηλαδή ακριβώς οι ίδιες όπως και του κάθε ενός από του 2.097.152 πιθανούς συνδυασμούς.
Άλλο ένα παράδειγμα που καταδεικνύει ότι τα μαθηματικά και η ανθρώπινη διαίσθηση είναι αντικρουόμενες έννοιες, είναι το πρόβλημα των γενεθλίων. Από την 1η Ιανουαρίου μέχρι και την 31η Δεκεμβρίου είναι 366 μέρες, συμπεριλαμβανομένης και της 29ης Φεβρουαρίου. Άρα για να είμαστε 100% σίγουροι ότι θα βρούμε τουλάχιστον δύο άτομα με κοινή μέρα γενεθλίων, χρειαζόμαστε το λιγότερο 367 άτομα, δηλαδή αυτούς του 366 και ακόμα έναν. Ενώ το παραπάνω παράδειγμα είναι πλήρως κατανοητό και μέσα στην «κοινή λογική» δεν ισχύει το ίδιο για τον μικρότερο αριθμό ατόμων που απαιτούνται ώστε η πιθανότητα να βρούμε τουλάχιστον δύο άτομα με την ίδια μέρα γενέθλιων να είναι 99%. Σκεφτείτε το λίγο, κάντε μια πρόβλεψη και μετά διαβάστε το άρθρο πρόβλημα των γενεθλίων για να δείτε πόσο έξω πέσατε.
Πόσες φορές ακούσατε Χριστούγεννα να επαναλαμβάνεται η φράση «αν έχεις τύχη, διάβαινε…». Σίγουρα πολλάκις τέτοιες μέρες που, εορταστική αδεία, τα τυχερά παιχνίδια έχουν την τιμητική τους. Είναι τότε που αγοράζουμε ελπίδα ή αλλιώς ένα λαχείο, ένα δελτίο των παιχνιδιών του ΟΠΑΠ, ένα στροβίλισμα στον δίσκο της ρουλέτας ή μια τράπουλα στην πράσινη τσόχα. Κάθε τόσο όμως επανέρχονται σφαλερές απόψεις σχετικά με τα τυχερά παιχνίδια, με προεξάρχουσα την αντίληψη ότι υπάρχει στρατηγική επιτυχίας. Ο κ. Γιώργος Παπαχρήστου, επίκουρος καθηγητής στο Τμήμα Οικονομικών Επιστημών στο Αριστοτέλειο Πανεπιστήμιο Θεσσαλονίκης, επισημαίνει ότι «δεν μπορεί κανείς να νικήσει την τύχη. Είναι όμως δυνατόν να νικήσει τους συμπαίκτες του, αν γνωρίζει ή μπορεί να πιθανολογήσει τις επιλογές τους. Γνωρίζοντας πώς παίζουν οι υπόλοιποι παίκτες, κάποιος παίκτης μπορεί να πετύχει υψηλότερα κέρδη στοιχηματίζοντας αντίθετα στο πλήθος (betting against the crowd)». Και αυτό δεν μπορεί να συμβεί ούτε στα λαχεία ούτε στη ρουλέτα ούτε στο Μπλακ Τζακ και σε τέτοιου είδους παιχνίδια.
Ο καθηγητής τονίζει ότι στρατηγική επιτυχίας μπορεί να υπάρξει στα τυχερά παιχνίδια τύπου Λόττο και Τζόκερ, όπου όταν κάποιος γνωρίζει ποιοι είναι οι δημοφιλείς αριθμοί στους παίκτες (δηλαδή πόσο συχνά ποντάρονται οι διάφοροι αριθμοί), μπορεί να επιλέξει αυτούς που προτιμώνται λιγότερο από τους συμπαίκτες του.
Ετσι, σε περίπτωση που βγουν αυτά τα νούμερα, μπορεί να κερδίσει περισσότερα λεφτά, γιατί θα υπάρχουν λίγες επιτυχίες. Επομένως, «υπάρχει στρατηγική επιτυχίας» σε σχέση με το να βρει κάποιος το δελτίο που θα έχει μεγαλύτερη προσδοκία κέρδους, σύμφωνα με τον κ. Παπαχρήστου, ο οποίος μάλιστα μας εξηγεί ότι η δυνατότητα αυτή έχει τεκμηριωθεί εμπειρικά σε δύο πρόσφατες έρευνες που έκανε και αφορούν το Λόττο στην Ελλάδα.
* Αντίπαλος οι συμπαίκτες
Στα παιχνίδια τύπου Λόττο και Τζόκερ ισχύουν τρεις απλές αρχές:
α) Η κληρωτίδα δεν έχει προτιμήσεις ούτε μνήμη (όλοι οι αριθμοί και οι συνδυασμοί αριθμών έχουν κάθε φορά την ίδια πιθανότητα κλήρωσης).
β) Οι παίκτες έχουν προτιμήσεις και μνήμη και
γ) Αντίπαλος δεν είναι η τύχη ούτε ο διοργανωτής, αλλά οι συμπαίκτες.
Οι προτιμήσεις των παικτών διαπιστώνονται εύκολα στις χώρες εκείνες (ΗΠΑ, Καναδάς) όπου δημοσιεύονται στατιστικές σχετικά με τη συχνότητα επιλογής των αριθμών από τους παίκτες. «Αυτό δηλαδή που διαπιστώνεται είναι η ύπαρξη δημοφιλών αριθμών (popular numbers). Οι παίκτες όμως έχουν και μνήμη. Και η μνήμη αυτή τους παίζει παιχνίδια! Ετσι,νομίζουν εσφαλμένα ότι αριθμοί που δεν έχουν βγει συχνά στο παρελθόν έχουν μεγαλύτερη πιθανότητα κλήρωσης στο μέλλον».
Κατά την πιο διαδεδομένη αντίληψη, γνωστή ως «σφάλμα του τζογαδόρου», «η τύχη γίνεται αντιληπτή ως μια αυτο-διορθωτική διαδικασία όπου αποκλίσεις προς μια κατεύθυνση επιφέρουν αντισταθμιστικές αποκλίσεις προς την άλλη». Λόγω της αντίληψης αυτής, τα άτομα επενδύουν χρόνο και πόρους στην πρόβλεψη μελλοντικών γεγονότων, είτε πρόκειται για τις τιμές των μετοχών είτε πρόκειται για τις κληρώσεις του Λόττο, και ενεργούν ανάλογα διαπιστώνει ο κ. Παπαχρήστου. «Αν και η αντίληψη δεν έχει επιστημονική βάση, έχει σημαντικά αποτελέσματα. Επιτρέπει την πρόβλεψη της συμπεριφοράς σε παιχνίδια όπου τα στοιχήματα είναι αμοιβαία, όπου δηλαδή το κέρδος ενός παίκτη είναι ζημιά για κάποιον άλλον (όπως το χρηματιστήριο αλλά και το Λόττο και το Τζόκερ)».
Είναι γνωστό ότι παίκτες του Λόττο παρακολουθούν τις συχνότητες με τις οποίες οι αριθμοί κληρώνονται και βάσει αυτών επιλέγουν τους δικούς τους αριθμούς. «Δεδομένου ότι οι “καθυστερημένοι” αριθμοί επιλέγονται περισσότερο, μεγαλύτερος αριθμός νικητριών στηλών ή, ισοδύναμα, χαμηλότερα κέρδη ανά νικήτρια στήλη σε κάθε κατηγορία κερδώνσυνοδεύουν την κλήρωση των αριθμών αυτών. Η υπόθεση αυτή μπορεί να ελεγχθεί στατιστικά με βάση την ιστορία των κληρώσεων Λόττο στην Ελλάδα» σημειώνει ο κ. Παπαχρήστου. Και εξηγεί: «Αν η επιλογή των αριθμών στα δελτία ήταν τυχαία, τότε ο θεωρητικά αναμενόμενος αριθμός επιτυχιών θα ήταν συνάρτηση της πιθανότητας επιτυχίας και του αριθμού των στηλών. Αν, λόγου χάριν, έχουν συμπληρωθεί 30 εκατομμύρια στήλες, τότε ο θεωρητικά αναμενόμενος αριθμός στηλών με έξι επιτυχίες είναι 30.000.000/13.983.816=2,14 (δεδομένου ότι η πιθανότητα να έχει κανείς εξάρι στο Λόττο είναι 1 στις 13.983.816). Τι συμβαίνει όμως όταν η επιλογή των αριθμών δεν είναι τυχαία;Για παράδειγμα, τι συμβαίνει όταν οι παίκτες επιλέγουν τους αριθμούς με τη μεγαλύτερη καθυστέρηση; Στην περίπτωση αυτή, ο αριθμός των επιτυχιών θα είναι σημαντικά μικρότερος από τον θεωρητικό αριθμό, όταν είναι μικρότερη η μέση καθυστέρηση των αριθμών που κληρώνονται». Η σχέση αυτή μεταξύ της διαφοράς πραγματικού από θεωρητικό αριθμό επιτυχιών και καθυστέρησης έχει εκτιμηθεί και ελεγχθεί στατιστικά για το Λόττο σε ένα δείγμα κληρώσεων από το 1990 ως τον Ιούλιο του 1997. Η υπόθεση συνεπώς ότι οι παίκτες του Λόττο υπόκεινται στο σφάλμα του τζογαδόρου έχει επαληθευτεί στην Ελλάδα. «Το συμπέρασμα συνεπώς είναι ότι υπάρχει τρόπος να βελτιώσει κανείς (όχι όλοι) τις επιδόσεις του στο παιχνίδι στοιχηματίζοντας αντίθετα προς το πλήθος, παίζοντας δηλαδή τους αριθμούς που κληρώθηκαν πρόσφατα».
* Ο ηλεκτρονικός τζόγος

Στην εποχή της τεχνολογίας και της επικοινωνίας on line, ο τζόγος έχει ανοίξει μια νέα αγορά. Η βιομηχανία της τύχης στον κυβερνοχώρο αναδεικνύεται σε κερδοφόρα επένδυση. Σύμφωνα με έκθεση της εταιρείας συμβούλων Datamonitor, που δημοσιεύθηκε φέτος στο Λονδίνο, ο τζόγος μέσω Internet θα φθάσει στα δέκα δισεκατομμύρια δολάρια τα επόμενα πέντε χρόνια, ενώ σήμερα είναι 535 εκατομμύρια δολάρια.
Η προϋπόθεση για να παίξει κάποιος είναι να έχει υπολογιστή συνδεδεμένο με μόντεμ και βέβαια πιστωτική κάρτα. Στην Ελλάδα εταιρεία θυγατρική της αμερικανικής πολυεθνικής εταιρείας τηλεπικοινωνιών και ιδιοκτήτριας καζίνων στο Λας Βέγκας απευθύνεται στο ελληνικό κοινό αναφέροντας:«Η εταιρεία μας προσφέρει προκαθορισμένες αποδόσεις σε όλα τα αθλήματα από ευρωπαϊκό και αμερικανικό ποδόσφαιρο,ευρωπαϊκό και αμερικανικό μπάσκετ,ΝΒΑ,γκολφ,τένις,σκι,Φόρμουλα 1,στίβο και σε άλλα αθλητικά γεγονότα,καθώς επίσης για εκλογές κυβερνήσεων,φεστιβάλ τραγουδιού,βραβεία Οσκαρ και οτιδήποτε άλλο ενδιαφέρει και ζητήσουν οι πελάτες της». Μάλιστα, στο σχετικό site (στην ηλεκτρονική διεύθυνση http: //www.betshop.com/fr-gr1. htm) επισημαίνει ότι «η ελληνική νομοθεσία απαγορεύει να οργανώνεται το στοίχημα στην Ελλάδα,αλλά δεν απαγορεύει στους Ελληνες ως πολίτες της Ευρωπαϊκής Ενωσης να παίζουν στην Αγγλία,όπου η νομοθεσία το επιτρέπει και είναι νόμιμο».
Μαύρο, κόκκινο και οι 37 μαγικοί αριθμοί
Τι γίνεται όμως με τα παιχνίδια στο καζίνο; Οπως έχει επισημανθεί από διεθνείς στατιστικές, η ρουλέτα δίνει στο καζίνο κέρδος ίσο με το 20% του τζίρου, το Μπλακ Τζακ το 26%, το μπάνγκο πούντο (παραλλαγή του μπακαρά) το 14%, το σταντ πόκερ ή καρίμπιεν πόκερ πάνω από 40%, όπως και τα αμερικανικά ζάρια (κερδίζει το 7 και το 11). Ο παίκτης ξεχνά ότι στα τυχερά παιχνίδια ο διοργανωτής έχει το πάνω χέρι και όσοι τζογάρουν είναι «αιμοδότες». Οπως και στη γκανιότα των χαρτοπαικτικών λεσχών, έτσι και στο καζίνο υπάρχει η «μαθηματική γκανιότα», που σημαίνει ότι σε κάθε γύρα της μπίλιας στη ρουλέτα, έτσι κι αλλιώς το τραπέζι θα έχει κέρδος 2,7% (αφού ποντάρονται 37 νούμερα, αλλά πληρώνονται 36).
Η εικόνα του παίκτη που καταγράφει σε μπλοκάκι τους προηγούμενους αριθμούς και σημειώνει κάθε καινούργιο αποτέλεσμα στη ρουλέτα είναι συνήθης. Η μέθοδος αυτή μπορεί να αποδειχθεί αποτελεσματική;
Ο Νόμος των Μεγάλων Αριθμών αποδεικνύει μαθηματικώς ότι, εξετάζοντας ένα μεγάλο πλήθος αποτελεσμάτων της ρουλέτας, οι 37 αριθμοί εμφανίζονται με την ίδια συχνότητα. Το ίδιο ισχύει και με το μαύρο και κόκκινο. Οι πιθανότητες να βγει οποιοσδήποτε αριθμός ή να έρθει κόκκινο και μαύρο είναι μοιρασμένες. Θυμάστε το τεστ λογικής που ρωτάει «αν έχετε ένα κέρμα και παίζοντας “κορόνα – γράμματα” έρχεται εννιά συνεχείς φορές “κορόνα”, πόσες πιθανότητες έχει να έρθει “γράμματα” τη δέκατη φορά»; Η απάντηση είναι 50%, όσες πιθανότητες δηλαδή έχει να έρθει και “κορόνα”! Η τακτική λοιπόν να διπλασιάζει κανείς το ποσό που ποντάρει στο μαύρο, για παράδειγμα, όσο βλέπει ότι καθυστερεί να βγει, ευελπιστώντας πως την επόμενη φορά θα έρθει, το πιο πιθανό είναι να σας κάνει να ξεμείνετε από λεφτά παρά να ρεφάρετε…
Το ίδιο αναποτελεσματική είναι η στρατηγική της… πίτσας, η λεγόμενη και «μέθοδος των τόξων». Επειδή οι αριθμοί στη ρουλέτα είναι σκορπισμένοι και όχι τοποθετημένοι διαδοχικά από το μηδέν ως το 36, η μέθοδος αυτή καλεί τον παίκτη να ποντάρει σε αριθμούς που αντιστοιχούν σε γειτονικές φέτες στον δίσκο της ρουλέτας (η πίτσα που λέγαμε). Δίνεται λοιπόν η εντύπωση ότι, αντί να ποντάρει, για παράδειγμα, στη σειρά αριθμών από το ένα ως το 12 (που είναι διασκορπισμένα), καλύτερο είναι να ποντάρει δώδεκα γειτονικούς αριθμούς στη ρουλέτα-πίτσα, για να καλύψει έτσι το ένα τρίτο της. Οποία φενάκη!… Η τύχη χαμογελά, αλλά ξέρει ακριβώς το ίδιο να σε κάνει να κλαις. Τύχη είναι αυτή… Το ίδιο συμβαίνει με το Μπλακ Τζακ, το γνωστό μας «είκοσι ένα». Χριστούγεννα – Πρωτοχρονιά: 13 δισ. δρχ. στα καζίνα
Πέρυσι, κατά τη διάρκεια των Χριστουγέννων και της Πρωτοχρονιάς, ο συνολικός τζίρος στα καζίνα της Ελλάδας ξεπέρασε τα 13 δισεκατομμύρια δραχμές, αφού περισσότεροι από 50.000 παίκτες πέρασαν από τα καζίνα εκείνες τις μέρες. Σύμφωνα με τα στοιχεία της Εθνικής Στατιστικής Υπηρεσίας, το 1997 οι Ελληνες δαπάνησαν περίπου 425,6 δισεκατομμύρια δραχμές στα καζίνα (273,8 δισ. δραχμές το 1996), ενώ συνολικά έπαιξαν 836,2 δισεκατομμύρια δρχ. στα τυχερά παιχνίδια όλων των κατηγοριών (λαχεία, Ξυστό, Τζόκερ, ΠΡΟ-ΠΟ, Λόττο, καζίνο, ιππόδρομος κ.ά.), αύξηση κατά 23,3% σε σχέση με το 1996 (678,2 δισ. δραχμές).
Ως προς τη συμμετοχή στα παιχνίδια του ΟΠΑΠ, οι νησιώτες μας, Ροδίτες, Κώοι και Κερκυραίοι, κρατούν τα σκήπτρα. Σύμφωνα με τα στοιχεία της στατιστικής υπηρεσίας του Οργανισμού Προγνωστικών Αγώνων Ποδοσφαίρου, η μέση ετήσια συμμετοχή ανά κάτοικο, κατά τα έτη 1995, 1996 και 1997, ήταν 60.000 δραχμές περίπου για τη Ρόδο, 43.000 δραχμές για την Κω, 42.000 δραχμές για την Κέρκυρα, 37.500 δραχμές για το Κιλκίς και τη Σπάρτη, 36.500 δραχμές για την Καστοριά. Η κατά κεφαλή συμμετοχή για όλη τη χώρα για το δεκάμηνο 1998 κατά παιχνίδι είναι 3.568 δραχμές στο ΠΡΟ-ΠΟ, 3.480 δραχμές στο Λόττο, 1.462 δραχμές στο Πρότο, 269 δραχμές στο Προπογκόλ και 6.192 δραχμές στο Τζόκερ. Το σύνολο των καθαρών εισπράξεων του δεκάμηνου 1998, όσον αφορά τα παιχνίδια του ΟΠΑΠ, ήταν 162.356.815.957 δραχμές.
Παρασκευή, 23 Οκτωβρίου 2015